[백준] 1707 이분 그래프 자바
🐙 문제
https://www.acmicpc.net/problem/1707
이 문제는 " 이분 그래프 " 의 뜻을 잘 이해해야한다.
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 라 부른다.
쉽게 설명하자면, 그래프의 노드들을 바구니 A와 바구니 B에 나눠서 담는다고 하자.
이때 같은 바구니에 담긴 노드들끼리는 인접하면 안된다는 의미이다.
그래프가 예시로 주어졌을때, 노드를 번갈아 바구니 A,B에 나누어서 담아보면 된다.
[입력예시]
2 // 테스트 케이스 개수
3 2 // case1 : 노드의 개수, 엣지의 개수
1 3
2 3
4 4 // case2 : 노드의 개수, 엣지의 개수
1 2
2 3
3 4
4 2
🐙 풀이과정
이분 그래프인 case
첫번째 케이스를 그림으로 나타내면 아래와 같다

그리고 바구니 A,B 를 만든다.
먼저 바구니 A에 노드 1을 담는다. ( A,B 아무거나 상관없음)

노드3으로 이동하여, 현재 바구니의 값과 반대인 바구니 B에 담는다. ( 바구니는 A,B 두개 밖에 없기 때문에 A 가 아니라면 B에 담아야한다)

방문하지 않은 노드2로 이동하여, 현재 바구니 값(B)와 반대인 바구니 A에 값을 담는다

노드 1에서 시작하여 노드들을 바구니에 번갈아 가며 담았을때, 위의 그림과 같이 구분된다.
결과적으로 같은 바구니A에 담긴 노드1,2는 인접하지 않는다.
이러한 과정을 노드2에서 시작, 노드3에서 시작하더라도 항상 같은 바구니에 있는 노드들은 인접하지 않는다.
- 노드 2에서 시작한 경우

- 노드3에서 시작한 경우

따라서 이 그래프는 이분 그래프 라고 할 수 있다.
잘 이해가 안간다면 이분 그래프가 안되는 경우를 보고 이해해보자
이분 그래프가 아닌 case
문제의 예시2번째는 이분 그래프가 아닌 경우이다.
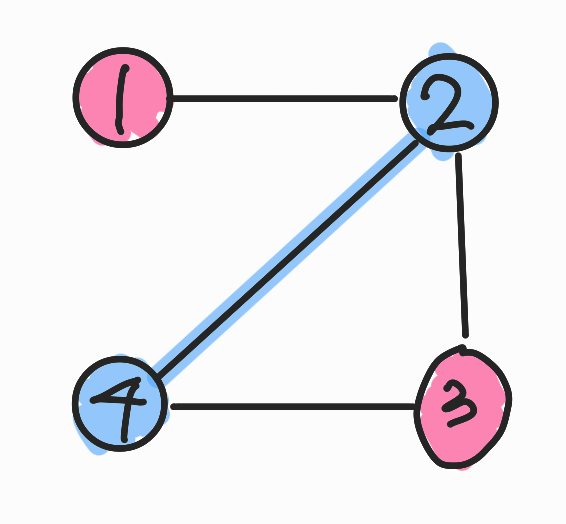
왜냐하면 위의 그림에서 나와있듯이, 2 → 3 → 4 가 사이클을 형성하고 있다.
그런데 4 → 2 의 경우, B에 담긴 노드4가 B에 담긴 노드2와 인접하고 있다. 즉, 같은 바구니에 담긴 노드들이 인접했다.
따라서 이 경우는 이분 그래프가 될 수 없다.
그렇다면 어떤 상황에 같은 바구니에 담긴 노드들이 서로 인접할까?
정답은 다음 경로에 있는 노드가, 현재 노드의 바구니와 동일한 경우이다.
현재 노드가 바구니 A에 담겨있는데, 다음으로 탐색할 노드도 바구니A에 담겨있다면 이 경우 이분 그래프의 정의에 위배되는 것이다.
- 임의의 노드 한점에서 DFS를 수행한다. ( 중요한 것은 모든 노드에서 수행해야한다는것!)
- 아직 방문하지 않은 노드라면, 현재 바구니의 값과 다른 바구니의 값으로 설정한다.
- 이미 방문한 노드라면, 해당 노드의 바구니의 값을 확인하여 현재 바구니의 값과 일치한다면 No를 출력, 현재 바구니의 값과 일치하지 않는다면 Yes를 출력한다.
🐙 코드
package 고자프_수업정리.그래프;
import java.io.*;
import java.util.*;
public class P48_이분그래프 {
static ArrayList<Integer>[] list; // 그래프 저장
static StringBuilder sb; // 결과를 저장
static String[] visited; // 방문 상태 저장
static final String NOT_VISITED = "N"; // 초기값 설정
static boolean isBipartiteGraph; // 이분 그래프 여부 확인 플래그
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int k = Integer.parseInt(br.readLine()); // 테스트 케이스 개수
sb = new StringBuilder();
for (int i = 0; i < k; i++) {
st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken()); // 정점 개수
int E = Integer.parseInt(st.nextToken()); // 간선 개수
// 그래프 초기화
list = new ArrayList[V + 1];
visited = new String[V + 1];
for (int j = 1; j <= V; j++) {
list[j] = new ArrayList<>();
visited[j] = NOT_VISITED;
}
// 그래프 생성
for (int j = 0; j < E; j++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
// 무방향 간선 추가
list[u].add(v);
list[v].add(u);
}
// 이분 그래프 판별
isBipartiteGraph = true; // 기본값
// 주어진 그래프가 연결그래프라는 보장 x -> 모든 노드에서 수행하기
for (int j = 1; j <= V; j++) {
if (visited[j].equals(NOT_VISITED)) {
checkBipartiteGraph(j, "A");
if(!isBipartiteGraph) break;
}
}
// 결과 저장
sb.append(isBipartiteGraph ? "YES" : "NO").append("\n");
}
// 결과 출력
bw.write(sb.toString());
bw.flush();
bw.close();
br.close();
}
static void checkBipartiteGraph(int x, String group) {
visited[x] = group; // 현재 노드를 방문 표시
String opposite = group.equals("A") ? "B" : "A"; // 반대 그룹 설정
for (int num : list[x]) {
if (visited[num].equals(NOT_VISITED)) { // 아직 방문하지 않은 노드
checkBipartiteGraph(num, opposite);
} else if (visited[num].equals(group)) { // 동일 그룹에 속할 경우
isBipartiteGraph = false; // 이분 그래프가 아님
return;
}
}
}
}
🧐 무방향 그래프로 저장하는 이유?
간선의 방향이 입력에서 명확히 주어지지 않으면 양방향 그래프로 처리하자.
🧐 모든 노드에서 탐색을 시작해야하는 이유?
문제의 조건에서 모든 노드들이 하나로 연결되어있다고 생각할 만한 부분은 없었기 때문에, 임의의 한 노드에서만 탐색을 하여서 이분 그래프인지를 따져선 안된다. 모든 노드에서 확인을 해줘야한다.
그래서 boolean isBipartiteGraph = true; 라는 변수를 이용하여 한번이라도 false 값으로 초기화 되면 , 그 그래프는 이분 그래프가 될 수 없도록 하는 것이다.
🐙 정리
이 문제는 간단히 정리하자면, 그래프를 이용한 DFS 응용문제이다.
왜 이 문제에서 왜 DFS를 사용하였고, 왜 두 그룹으로 나누는지에 대해서 생각해보면 좋을 것 같다.